Jian Liu Group @PKU
Theoretical Chemistry / Chemical Dynamics


Our research deals with quantum and semiclassical theories of chemical dynamics and thermodynamics for "real" molecular systems. Development of such theories/methods would lead to prediction of dynamic, spectroscopic, and thermodynamic properties where nuclear quantum effects (including zero point energy, tunneling, and coherence effects) become important at low temperatures and/or in real systems that contain light atoms such as hydrogen, helium, and even lithium. Typical examples include vibrational dynamics, ground-/excited-electronic-state proton transfer reactions, hydrogen bonding effects, H/D/T isotopic substitution, separation, and fractionation, and many other phenomena (of importance of nuclear quantum effects) in chemical, biological, and materials systems. In addition to infrared (IR) and Raman spectroscopy, elastic and inelastic neutron scattering, high-resolution scanning tunneling microscopy, and other experimental methods, developing theories and computational tools to understand these phenomena or experimental results at the atomistic level presents challenging frontiers in modern physical chemistry.
We are focused on developing new theory, methods and models, and also on applying them to real molecular systems. Current primary interests are
Phase space formulations of quantum mechanics
Quantum/classical statistical mechanics
Efficient integrators/algorithms for molecular dynamics and path integral molecular dynamics
Path integral molecular dynamics for nonadiabatic systems
Quantum dynamics and spectroscopy for complex/large systems
Path integral Liouville dynamics
Equilibrium continuity dynamics
Semiclassical dynamics
Nonadiabatic field
AI for quantum dynamics and statistical mechanics
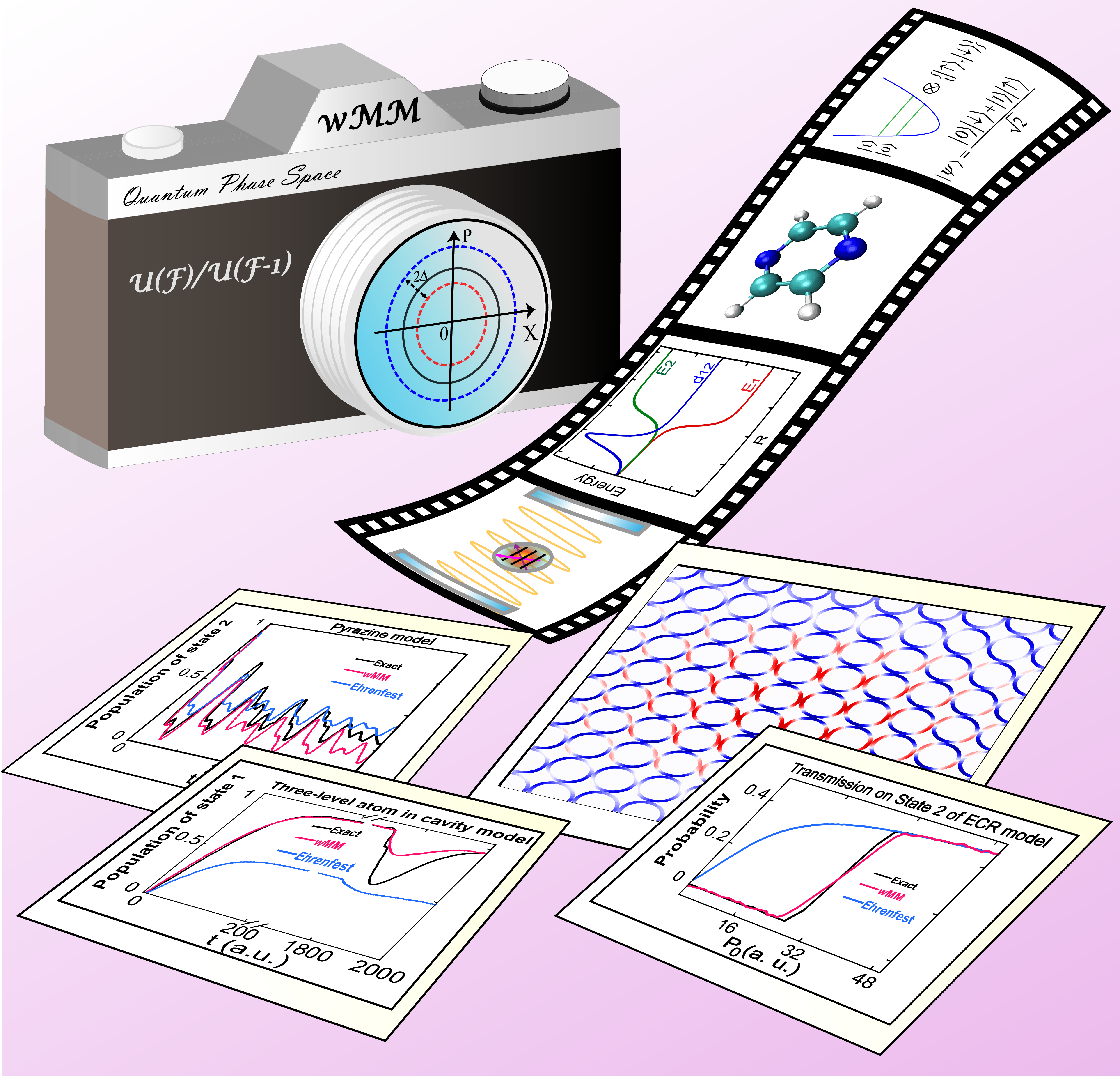
Phase space with coordinate-momentum variables bridges a rigorous formulation of classical mechanics and an exact interpretation of quantum mechanics. Conventional infinite coordinate-momentum phase space had been developed for systems with continuous degrees of freedom. We have proposed a generic framework to construct rigorous representations on constraint coordinate-momentum phase space (CPS) for F-state quantum systems, where exact equations of motion on phase space are simply linear and that the sum of state population is one is satisfied for each phase point.
In the CPS formulation, creation and annihilation operators are defined such that the space is complete for any combined excitation. Commutation and anti-commutation relations are then naturally derived, which show that the underlying degrees of freedom are neither bosons nor fermions. It leads to a generalized commutation relation with a commutator matrix. The CPS formulation with commutator variables is diffeomorphic to the complex Stiefel manifolds. By establishing CPS for discrete degrees of freedom and employing infinite phase space for continuous DOFs, we have developed the exact generalized coordinate-momentum phase space formulations for composite systems in chemistry, physics, information, etc.
It lays the solid foundation of developing consistent trajectory-based nonadiabatic dynamics methods. It offers a novel means to derive and understand isomorphic models where electronic and nuclear DOFs are treated on the same footing as pioneered by the Meyer-Miller-Stock-Thoss mapping Hamiltonian model. We have used a complex Stiefel manifold U(F)/U(F-1) and the Abel integral equation to construct a new class of exact phase space representations of two-state systems and proved that the heuristic Cotton-Miller triangle window function approach is a special case of this class.
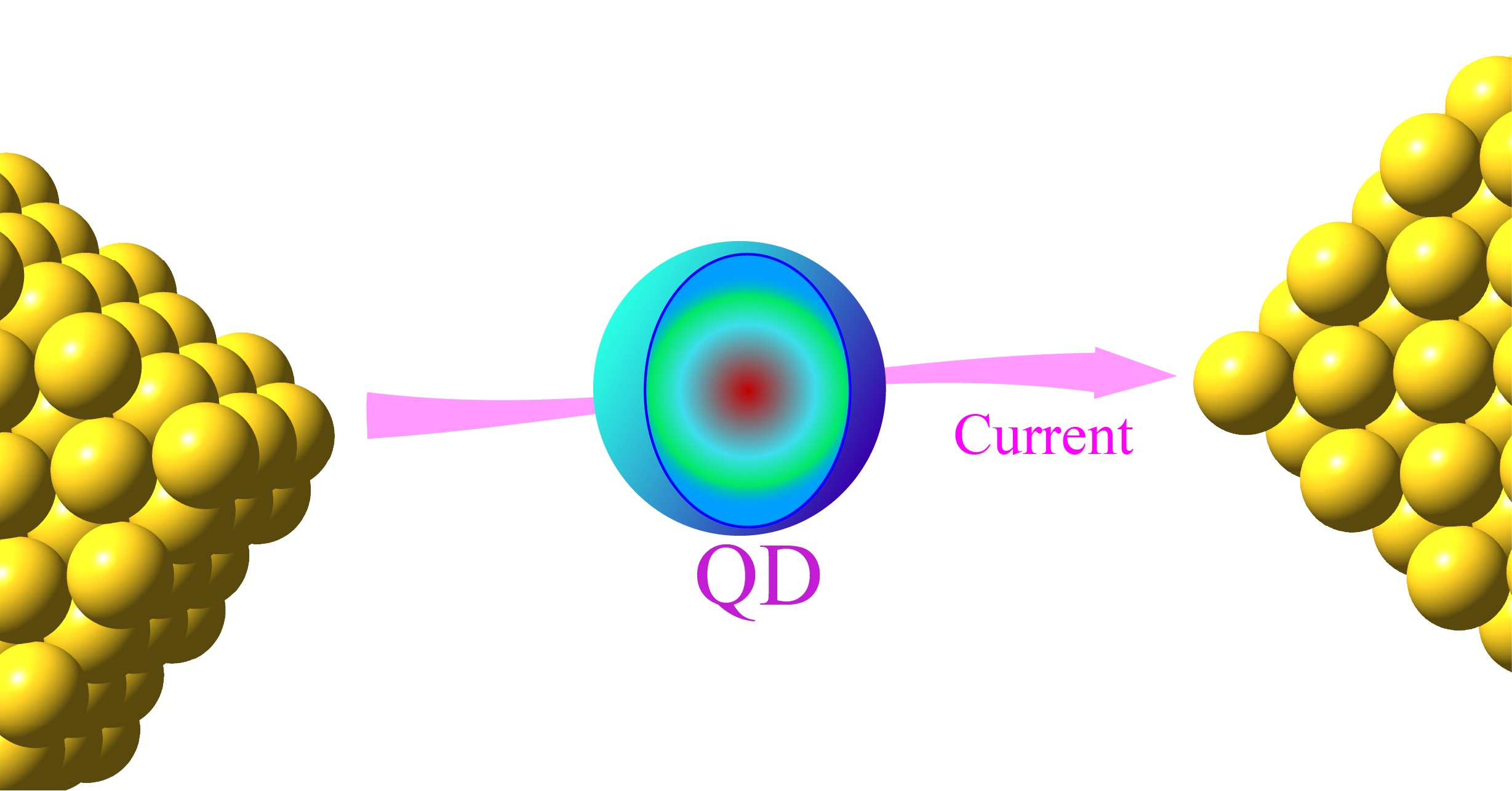
We have further introduced the isomorphism between the multi-state Hamiltonian and the second-quantized many-electron Hamiltonian (with only 1-electron interactions) and demonstrated that all methods developed for the former can be used for the latter, and vice versa. It indicates that phase space mapping approaches for multi-state nonadiabatic systems can be directly used for studying nonequilibrium quantum transport processes, e.g., the electronic current of the resonant level (Landauer) model for a quantum dot state coupled to two electrodes, the carrier mobility of the Holstein model for organic semiconductors, and so on.
The relevant peer-reviewed papers are
The Journal of Chemical Physics, 145, 204105 (2016) [http://dx.doi.org/10.1063/1.4967815]
The Journal of Chemical Physics, 146, 024110 (2017) [http://dx.doi.org/10.1063/1.4973708]
The Journal of Chemical Physics, 151, 024105 (2019). [https://doi.org/10.1063/1.5108736]
The Journal of Physical Chemistry Letters, 12, 10, 2496–2501 (2021) [https://pubs.acs.org/doi/full/10.1021/acs.jpclett.1c00232]
The Journal of Physical Chemistry A, 125, 31, 6845–6863 (2021) [https://doi.org/10.1021/acs.jpca.1c04429]
Accounts of Chemical Research, 54, 23, 4215–4228 (2021) [https://doi.org/10.1021/acs.accounts.1c00511]
Wiley Interdisciplinary Reviews-Computational Molecular Science, e1619 (2022) [https://doi.org/10.1002/wcms.1619][Supporting Information]
Chinese Journal of Chemical Physics, 37, 230-254 (2024) [https://doi.org/10.1063/1674-0068/cjcp2403033]
Fundamental Research (ASAP) [https://doi.org/10.1016/j.fmre.2025.09.013]
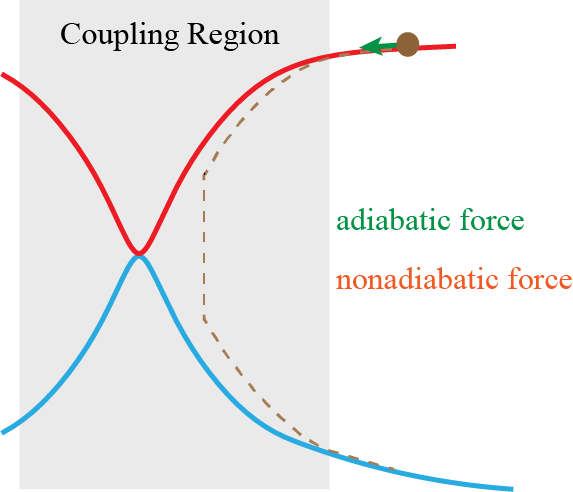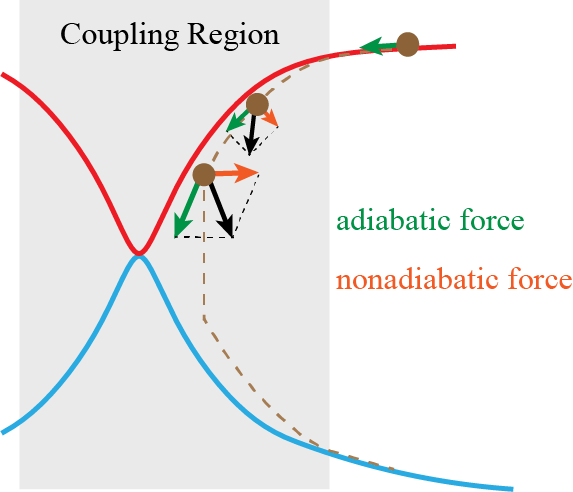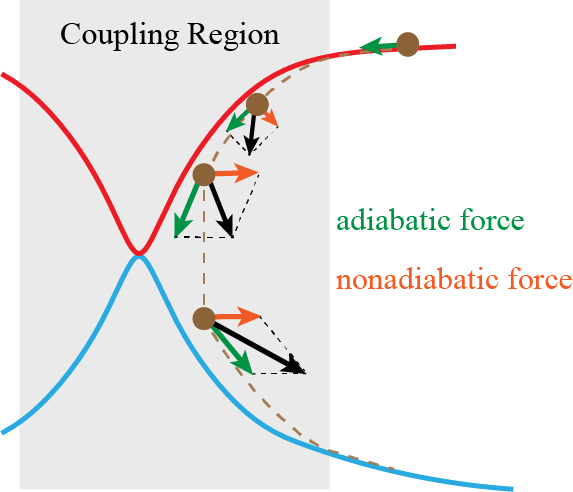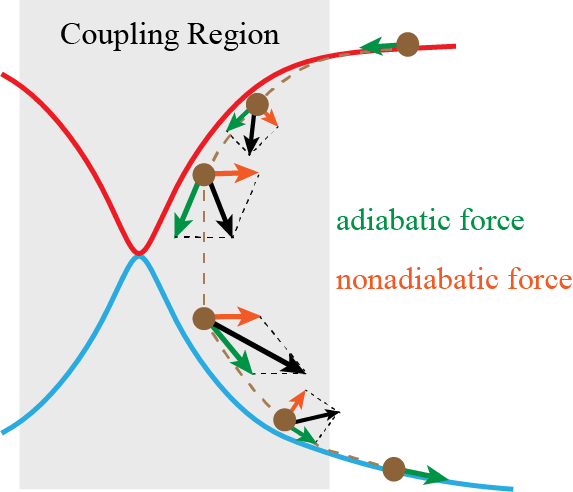
We have proposed nonadiabatic field (NaF), a conceptually novel approach for nonadiabatic dynamics with independent trajectories on quantum coordinate-momentum phase space. NaF involves the nonadiabatic force arising from the nonadiabatic coupling between different electronic states, in addition to the adiabatic force contributed by a single adiabatic electronic state. NaF is capable of faithfully describing the main features of the quantum mechanical behavior of both electrons and nuclei in nonadiabatic transition processes in a broad regime, from systems where the relevant electronic states keep coupled in a wide range and the nonadiabatic force plays an important role, for which it is difficult for surface hopping approaches to describe relatively-long time behavior, to systems where the bifurcation characteristic of nuclear motion is essential, which Ehrenfest(-like) dynamics methods fail to capture. NaF has been used to study population dynamics, electron transfer reaction rates, carrier mobilities, electronic spectra, cavity-modified dynamics for both gas phase and condensed phase systems.
The relevant peer-reviewed papers are
The Journal of Physical Chemistry Letters, 15, 2, 644-658 (2024) [https://doi.org/10.1021/acs.jpclett.3c03385][Supporting Information]
The Journal of Physical Chemistry Letters, 15, 20, 5452-5466 (2024) [https://doi.org/10.1021/acs.jpclett.4c00793][Supporting Information]
Journal of Chemical Theory and Computation, 21, 8, 3775-3813 (2025) [https://doi.org/10.1021/acs.jctc.5c00181][Supporting Information]
We were the first to develop a practical quantum dynamics method satisfying the two critical fundamental criteria: conservation of the quantum Boltzmann distribution for the thermal equilibrium system and being exact for any thermal correlation functions (of even nonlinear operators, i.e., nonlinear functions of position or momentum operators) in the classical and harmonic limits. The so-called path integral Liouville dynamics (PILD) [J. Chem. Phys. 140, 224107 (2014)] was derived from the elaborate combination of the imaginary time path integral and the three new theoretical frameworks that we formulated for generating trajectory-based dynamics methods in the quantum phase space [J. Chem. Phys. 134, 104101 (2011); 134, 104102 (2011); 134, 194110 (2011). Scientia Sinica Chimica, 46, 27 (2016)], of which the equilibrium continuity dynamics (ECD) category is the most fundamental.
PILD was applied to vibrational dynamics of several simple but representative real molecular systems (OH, water, ammonia, and methane) [J. Chem. Phys. 144, 034307 (2016)]. The dipole-derivative autocorrelation function was employed to obtain the infrared spectrum as a function of temperature and isotopic substitution. Comparison to the exact vibrational frequency shows that PILD produces a reasonably accurate peak position with a relatively small full width at half maximum. PILD offers a potentially useful trajectory-based quantum dynamics approach to compute vibrational spectra of molecular systems.
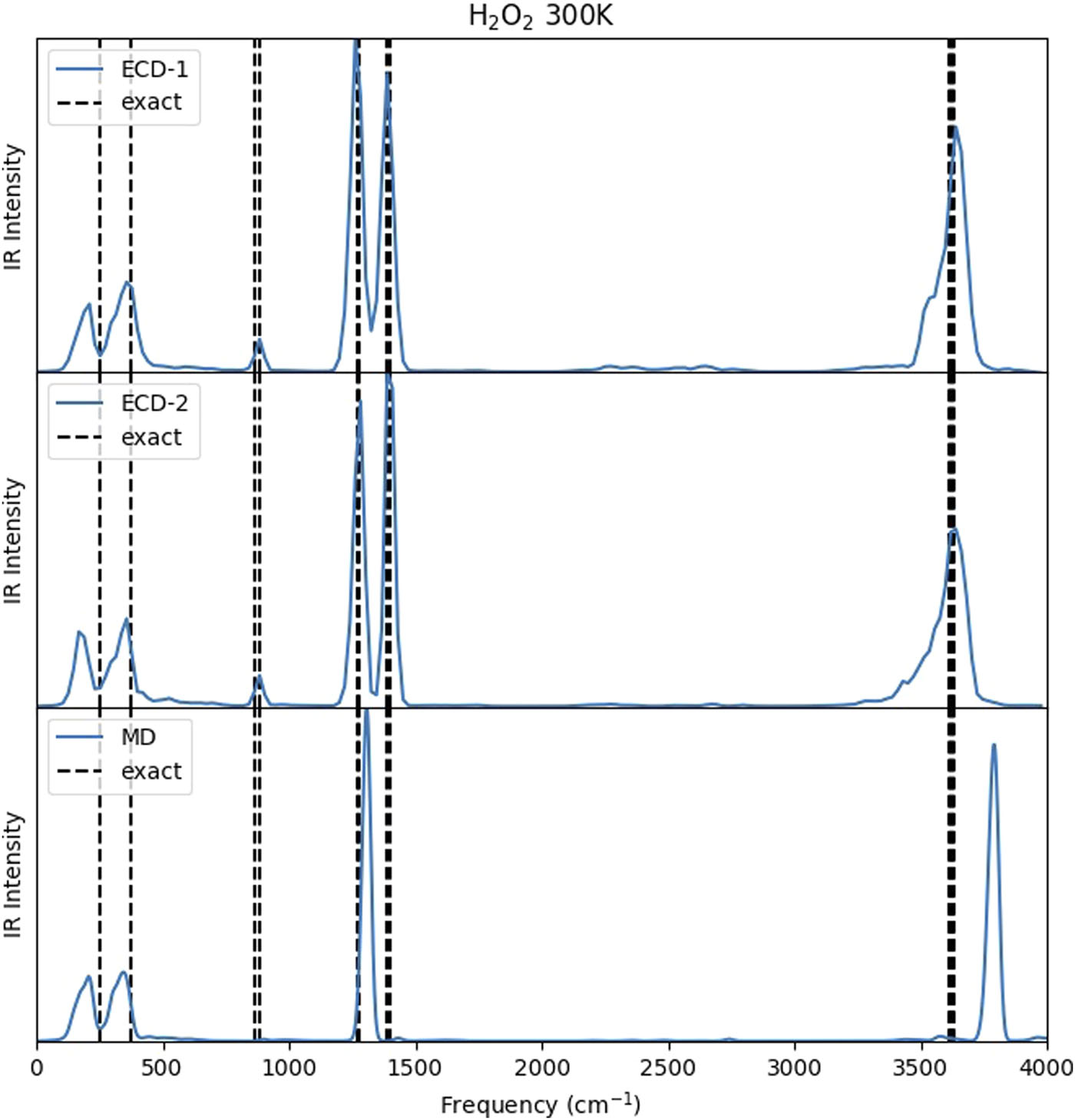
More recently, we have shown that the equations of motion of ECD involves only the zeroth-order term of an exact series expansion of the phase space propagator and that higher order corrections can consistently improve the accuracy [J. Chem. Phys. 154, 184104 (2021)]. The effective force and effective mass matrix are important elements in ECD. We introduce a machine learning approach for fitting these elements in quantum phase space, leading to a much more efficient integration of the equations of motion. Proof-of-concept applications to realistic molecules demonstrate that machine learning phase space dynamics approaches are possible as well as competent in producing reasonably accurate results with a modest computation effort.
The relevant peer-reviewed papers are
The Journal of Chemical Physics, 140, 224107 (2014) [https://doi.org/10.1063/1.4881518]
Scientia Sinica Chimica, 46, 27 (2016) [http://dx.doi.org/10.1360/N032015-00143]
The Journal of Chemical Physics, 144, 034307 (2016) [http://dx.doi.org/10.1063/1.4939953]
Chinese Journal of Chemical Physics, 33, 613 (2020) [https://doi.org/10.1063/1674-0068/cjcp2006099]
The Journal of Chemical Physics, 154, 184104 (2021) [https://doi.org/10.1063/5.0046689]
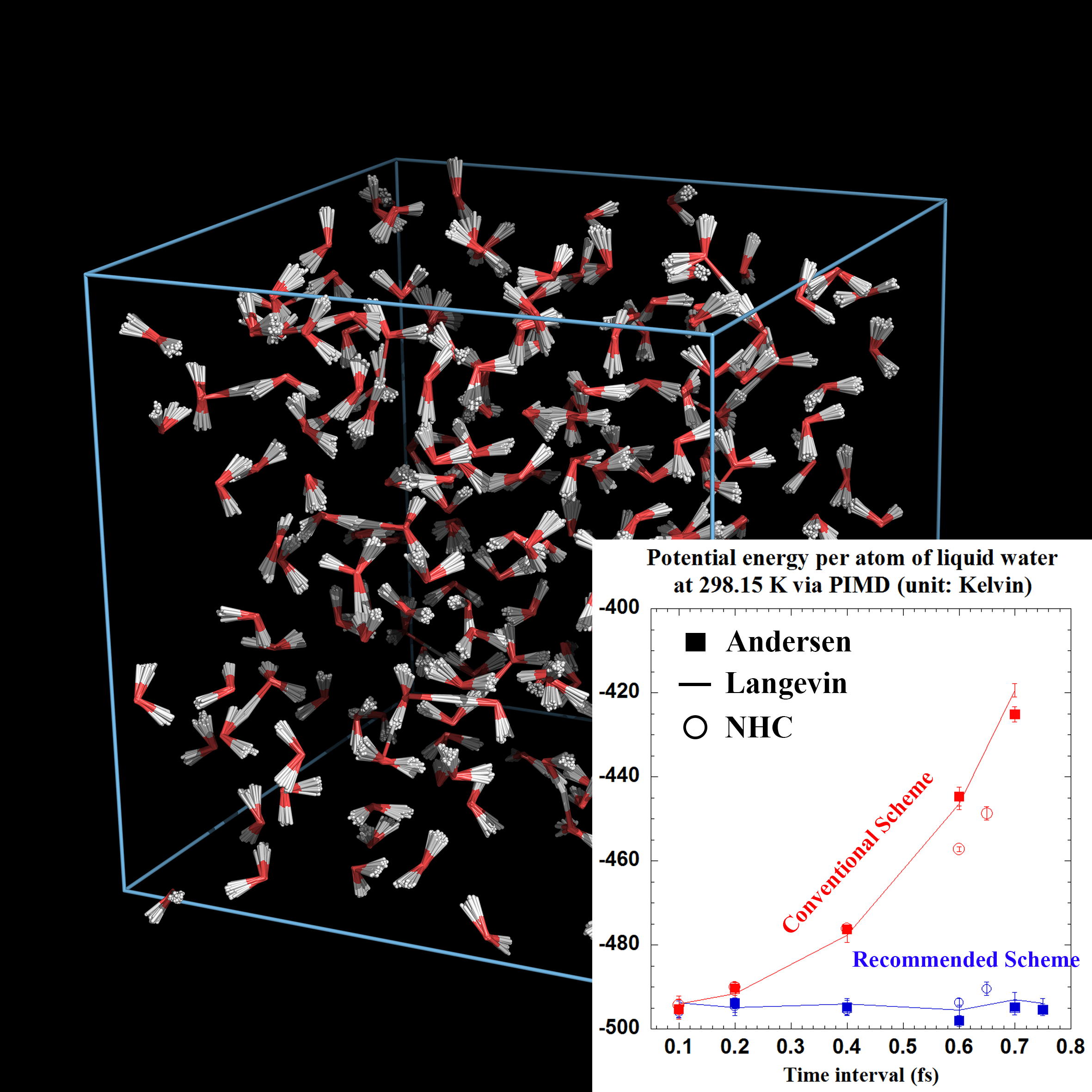
Path integral molecular dynamics (PIMD) is a prevailing computational tool to study nuclear quantum statistics for real molecular systems at thermal equilibrium. We have employed the phase space evolution operator to develop a unified framework that includes both stochastic and deterministic thermostatting algorithms, including such as the Andersen thermostat, Langevin dynamics, Nosé-Hoover chain (including Nosé-Hoover thermostat), etc. [J. Chem. Phys. 145, 024103 (2016); 147, 034109 (2017)] and covers various Monte Carlo or MD barostatting algorithms [J. Chem. Theory Comput. (2025)]. Compared to most conventional PIMD algorithms that can be unified in the “side”/“end” schemes of the framework, the "middle" thermostat scheme introduced by us significantly improves the sampling efficiency as well as accuracy for general molecular systems of canonical ensembles (with constant volume and temperature) as well as of isobaric-isothermal ensembles (with constant pressure and temperature). In addition to numerical examples for real systems, we have presented the analytical analysis to prove that the “middle” scheme leads to exact results for PIMD in the harmonic limit regardless of the thermostat parameter and of the finite time interval (as long as the propagation is stable).
In the unified framework we have revealed that, in addition to the usual density evolution, there exists another type of discrete evolution that may not correspond to a continuous, real dynamical counterpart of the Langevin equation [J. Chem. Phys. 147, 184104 (2017)]. This virtual dynamics case is also amenable to the desired Boltzmann distribution for various stochastic thermostatting methods [Chin. J. Chem. Phys. 30, 735 (2017)]. By analyzing the asymptotic distribution and characteristic correlation time, we have shown that, for good numerical performance in efficiency as well as accuracy, one may choose the thermostat parameter (of the “middle” scheme) in a wide range from around the optimal value to the high value limit.
We have further used the unified framework to develop a novel practical PIMD methodology in either of the diabatic and adiabatic representations for studying exact quantum statistics of large multi-electronic-state systems in thermal equilibrium when the Born-Oppenheimer approximation, Condon approximation, and harmonic bath approximation are no longer valid [J. Chem. Phys. 148, 102319 (2018)].
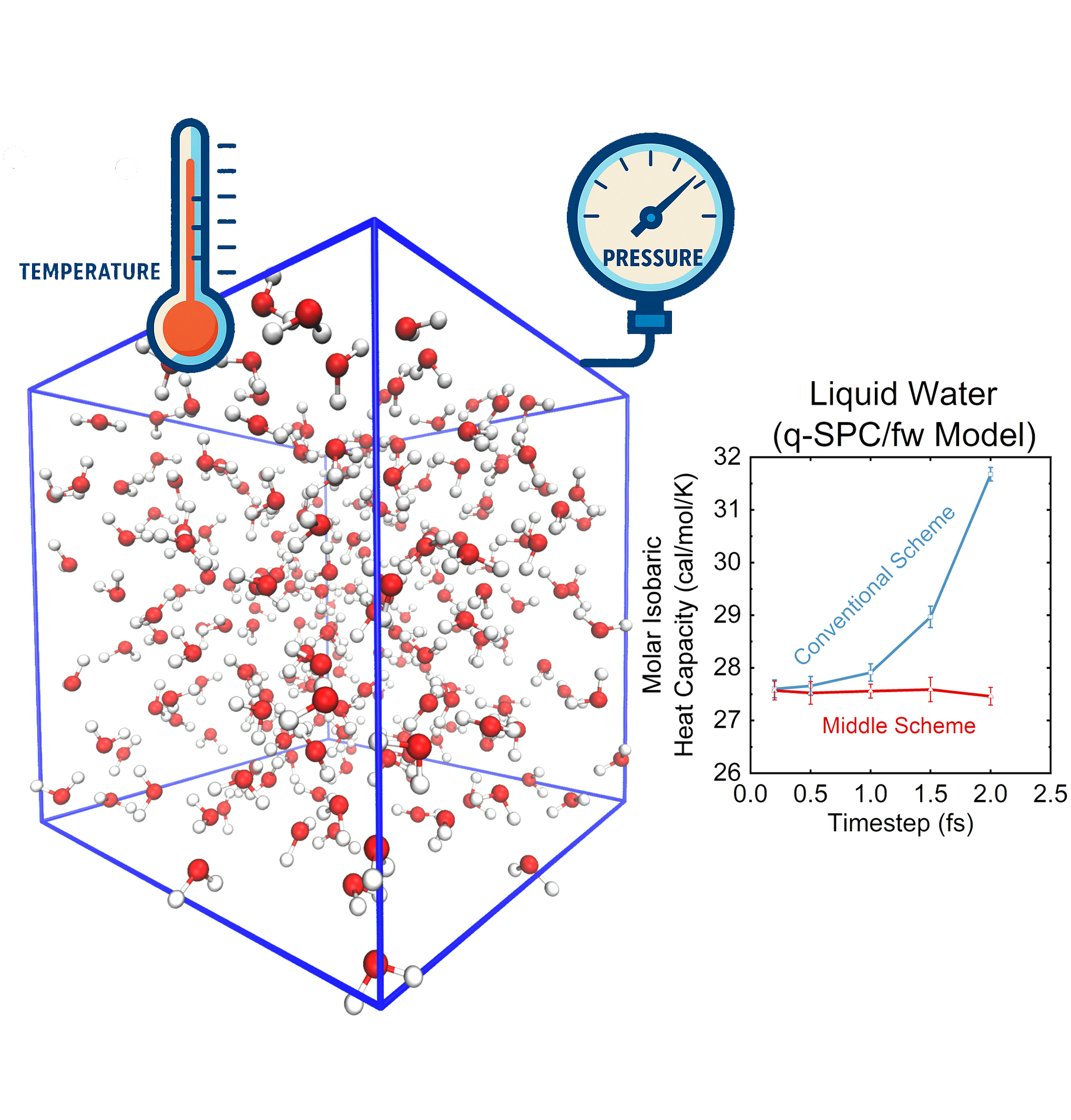
More recently, we have employed the "middle" scheme for molecular dynamics and path integral molecular dynamics simulations for efficient and accurate evaluation of density, isobaric heat capacity, isothermal compressibility, thermal expansion coefficient, and other physical properties of general molecular systems under conditions of controlled pressure and temperature.
Note: The unified "middle" thermostat scheme for canonical ensembles and that for isobaric-isothermal ensembles have been implemented in AMBER, AmberTools, and GROMACS. Please visit Tutorials for more details.
The relevant peer-reviewed papers are
The Journal of Chemical Physics, 145, 024103 (2016) [http://dx.doi.org/10.1063/1.4954990]
The Journal of Chemical Physics, 147, 034109 (2017) [http://dx.doi.org/10.1063/1.4991621]
The Journal of Chemical Physics, 148, 102319 (2018) [https://doi.org/10.1063/1.5005059]
The Journal of Chemical Physics, 147, 184104 (2017) [https://doi.org/10.1063/1.4996204]
Chinese Journal of Chemical Physics, 30, 735 (2017) [http://dx.doi.org/10.1063/1674-0068/30/cjcp1711223]
The Journal of Physical Chemistry A, 123, 28, 6056-6079 (2019) [https://doi.org/10.1021/acs.jpca.9b02771][pdf version][Highlighted in JPC Virtual Issue on New Tools and Methods]
Chinese Journal of Chemical Physics, 34, 6, 932-948 (2021) [https://doi.org/10.1063/1674-0068/cjcp2111242]
Chinese Journal of Chemical Physics, 35, 3, 516-536 (2022) [https://cps.scitation.org/doi/pdf/10.1063/1674-0068/cjcp2205089]
Journal of Chemical Theory and Computation (2025) (ASAP) [https://doi.org/10.1021/acs.jctc.5c00573]
Understanding vibrational spectra (infrared (IR) and Raman spectra) at the atomistic level is important for the elucidation of dynamical processes in complex/large molecular systems. The correlation approach offers a bridge to connect the microscopic motion to the experimental spectrum. Because the dipole moment/polarizability (or its time derivative) is often a highly nonlinear function of coordinates or/and momenta, we have employed the linearized semiclassical initial value representation for quantum dynamical simulations of liquid water (and heavy water) under ambient conditions based on an ab initio based, flexible, polarizable model. Besides applying our new PIMD algorithms in the “middle” scheme, we have proposed a new technique (by using the finite difference along the direction of a related vector) to significantly reduce the computational cost for preparing the initial condition for the correlation function.
It is shown that quantum dynamical effects play a critical role in reproducing the peaks in the intermediate region between the librational and bending bands, those between the bending and stretching bands, and the double-peak in the stretching band in the experimental isotropic Raman spectrum. In contrast, quantum dynamical effects are important but less decisive in the anisotropic Raman spectrum. By selectively freezing either the intramolecular O-H stretching or H-O-H bending mode, we demonstrate that the peak in the intermediate region (2000-2400 cm-1) of the isotropic Raman spectrum arises from the interplay of the stretching and bending motions while a substantial part of the peak in the same intermediate region of the anisotropic Raman spectrum may be attributed to the combined motion of the bending and librational modes.
The relevant peer-reviewed papers are
Molecular Physics, 116, 7-8, 755-779 (2018) [https://doi.org/10.1080/00268976.2018.1434907][Free eprints]
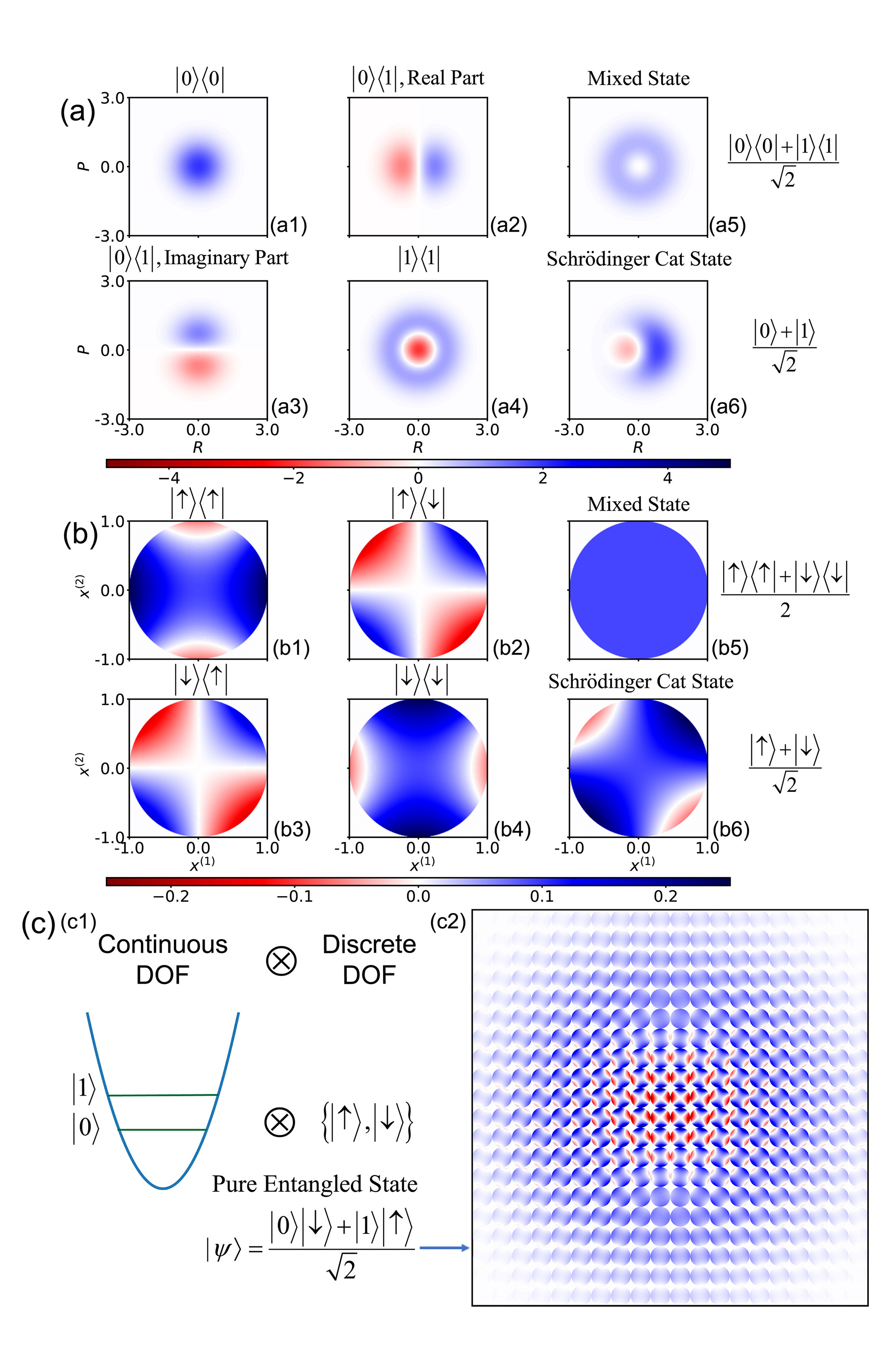
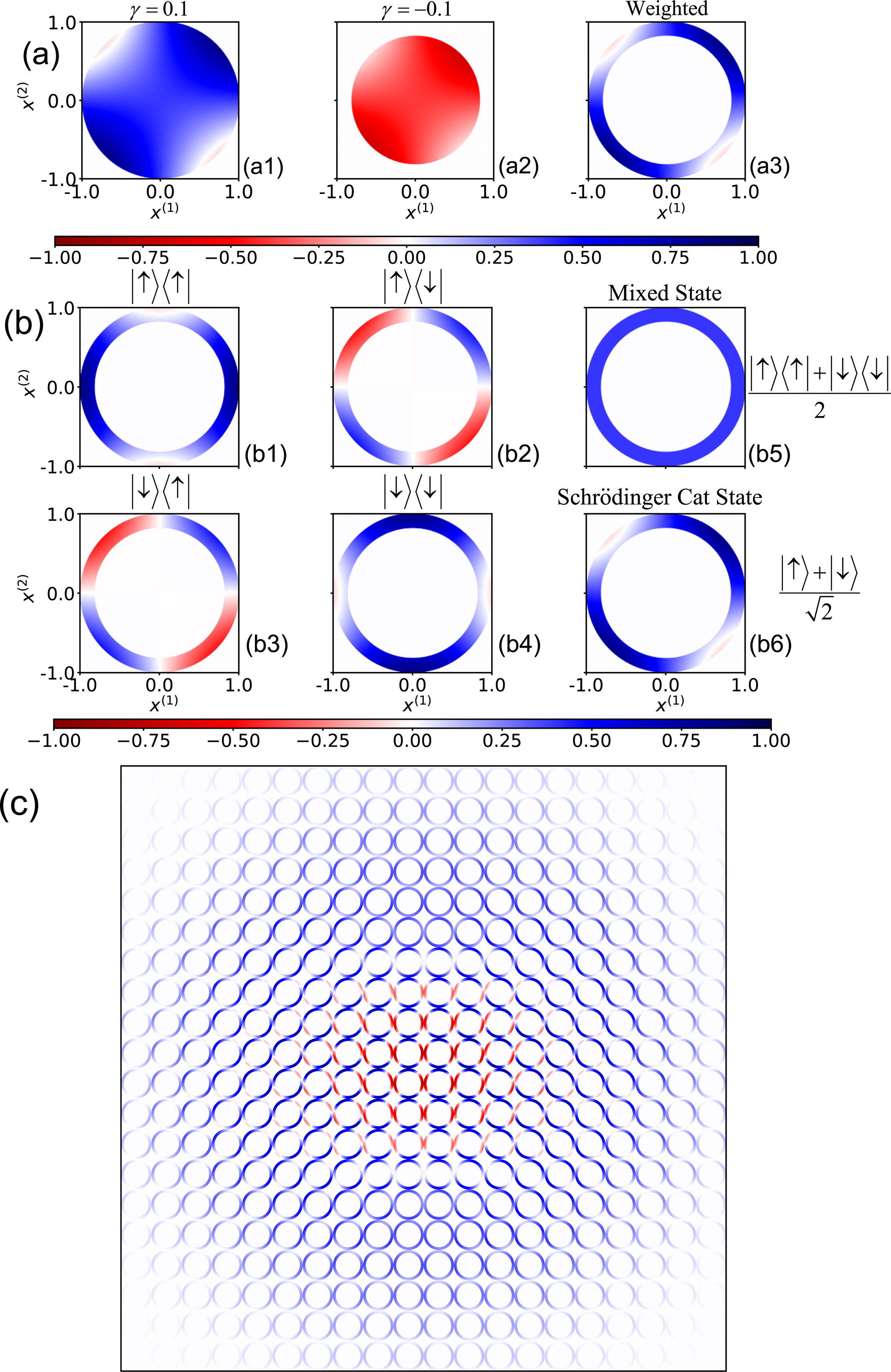
The generalized coordinate-momentum phase space formulation offers a potentially useful approach for describing correlations and nonclassical features of composite systems in quantum information.
The relevant peer-reviewed papers are
Wiley Interdisciplinary Reviews-Computational Molecular Science, e1619 (2022) [https://doi.org/10.1002/wcms.1619][Supporting Information]
The relevant peer-reviewed papers are
Journal of Chemical Theory and Computation, 21, 8, 3775-3813 (2025) [https://doi.org/10.1021/acs.jctc.5c00181][Supporting Information]